


Next: シミュレーションの手順
Up: Monte Carlo シミュレーション
Previous: マスター方程式とエルゴード性
定常状態では、Eq. (66)が成り立つ。
これを成分表示で書くと、
 |
(67) |
となるが、ここに
Eqs. (60)および(61)
を代入すると、詳細釣合(detailed balance)条件
 |
(68) |
を得る。
ここで  は平衡状態における状態
は平衡状態における状態 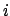 の出現確率であり、
の出現確率であり、
![\begin{displaymath}
P_{eq}(i) = \exp[-\beta H(i)]
\end{displaymath}](img209.png) |
(69) |
で与えられる。
即ち、状態 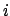 から
から  への遷移確率
への遷移確率
 とその逆に対して、関係式 (68)
が成り立つように遷移アルゴリズムを構成すれば、
定常Markov 過程として、Boltzmannウェイトに従う
アンサンブルが得られることになる。
とその逆に対して、関係式 (68)
が成り立つように遷移アルゴリズムを構成すれば、
定常Markov 過程として、Boltzmannウェイトに従う
アンサンブルが得られることになる。
次に、詳細釣合条件を満たすような遷移アルゴリズムを構成する
方法を二つ、紹介する。
- Metropolis 法
-
Metropolis 法は、詳細釣合条件を満たすようなアルゴリズムを
構成する一般的な方法である。
次に紹介する熱浴法に比べて効率は劣るものの、
熱浴法が構成できないような系に対しても適用できるため
重要である。
Matropolis 法では、まずアップデートすべき配位 に対し、候補となるアップデート後の配位
に対し、候補となるアップデート後の配位 を考える。
を考える。
 と
と  それぞれに対して Hamiltonian
を計算し、この候補配位
それぞれに対して Hamiltonian
を計算し、この候補配位  を、次の確率
を、次の確率
![\begin{displaymath}
P = \min\left\{1, e^{-\beta(H[\phi']-H[\phi])} \right\}
\end{displaymath}](img213.png) |
(70) |
で accept、即ちアップデート後の配位とする。
もし候補配位  が reject された場合には、
元の
が reject された場合には、
元の  をアップデート後の配位とする。
をアップデート後の配位とする。
- 熱浴法
-
Hamiltonian が局所的な項の和として表される場合
など、系がある条件を満たすとき、熱浴法(heat bath method)
が構成できる場合がある。
熱浴法では、今アップデートしたい自由度を  とする時、
これと相互作用する自由度を含む局所的な Hamiltonian
とする時、
これと相互作用する自由度を含む局所的な Hamiltonian
 を考える。
この時、
を考える。
この時、 以外の自由度を熱浴のように扱い、
以外の自由度を熱浴のように扱い、
 を確率
を確率
![$e^-\beta H[\phi_i;\phi_{j\neq i}]$](img215.png) で生成することが可能であれば、これを熱浴法とよぶ。
この局所的なアップデート繰り返す(sweepする)ことによって、
全系に対するアップデートを行う。
で生成することが可能であれば、これを熱浴法とよぶ。
この局所的なアップデート繰り返す(sweepする)ことによって、
全系に対するアップデートを行う。
Ising model の場合、
 |
(71) |
となる。
従って、格子点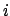 の周りのスピン自由度を調べて
の周りのスピン自由度を調べて
 を計算し、
を計算し、 区間の一様乱数
区間の一様乱数  を振って、
を振って、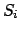 を
を
 |
(72) |
Hideo Matsufuru
2006-06-16
![]() に対し、候補となるアップデート後の配位
に対し、候補となるアップデート後の配位![]() を考える。
を考える。
![]() と
と ![]() それぞれに対して Hamiltonian
を計算し、この候補配位
それぞれに対して Hamiltonian
を計算し、この候補配位 ![]() を、次の確率
を、次の確率
