


Next: Ising モデル
Up: 統計物理と Ising モデル
Previous: 統計物理と Ising モデル
相互作用がハミルトニアン 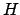 で記述される系があるとする。
自由度を一般に
で記述される系があるとする。
自由度を一般に  (i=1,2,...), 系のパラメターを
(i=1,2,...), 系のパラメターを  (a=1,2,...)とする。
例えば、強磁性体の場合、
(a=1,2,...)とする。
例えば、強磁性体の場合、 としては各格子点上のスピン自由度、
Kはスピン間の結合定数や、外からかけた磁場
としては各格子点上のスピン自由度、
Kはスピン間の結合定数や、外からかけた磁場 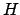 などを表す。
などを表す。
![\begin{displaymath}
H[\phi\, ; K] = - \sum_{i,j} J_{ij} \phi_i \cdot \phi_j
- H \sum_i \phi_i
\end{displaymath}](img8.png) |
(1) |
 は格子点
は格子点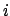 と
と のスピン間の結合定数である。
のスピン間の結合定数である。
系の熱力学的性質は、統計力学によって記述される。
統計力学では、
ミクロカノニカル・アンサンブル
(エネルギー、粒子数一定の下で等重率の原理に基づく)、
カノニカル・アンサンブル(熱浴と接触した系)、
グランドカノニカル・アンサンブル(熱浴、粒子浴と接触)
のような方法があるが、
Eq. (1)のような系の場合、
カノニカル・アンサンブルとして扱うのが適している。
カノニカル・アンサンブルでは、系の物理量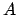 に関する統計
力学的平均値
に関する統計
力学的平均値
 は、アンサンブル平均、
は、アンサンブル平均、
![\begin{displaymath}
\langle A \rangle =
\frac{1}{Z} \mbox{Tr}( A e^{-\beta H[\phi]} )
\end{displaymath}](img14.png) |
(2) |
によって与えられる。
ここで  ,
,  は Boltzmann 定数、
は Boltzmann 定数、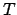 は温度。
は温度。
 の演算は、系の自由度のすべての場合についての和を
とることを表す。
系の自由度の値を1セット定めたものを、系の配位とよぶ。
の演算は、系の自由度のすべての場合についての和を
とることを表す。
系の自由度の値を1セット定めたものを、系の配位とよぶ。
 演算は、系のすべての配位について和を取ることを
意味している。
演算は、系のすべての配位について和を取ることを
意味している。
![$Z[K]$](img19.png) は分配関数と呼ばれる量で、
は分配関数と呼ばれる量で、
![\begin{displaymath}
Z[K] = \mbox{Tr}\, e^{-\beta H[\phi;K]}
\end{displaymath}](img20.png) |
(3) |
で与えられる。
系の熱力学的性質は自由エネルギー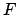 によって記述されるが、
これは分配関数によって次のように表される。
によって記述されるが、
これは分配関数によって次のように表される。
![\begin{displaymath}
F[K] = - k_BT \log Z[K]
\end{displaymath}](img22.png) |
(4) |
![$Z[K]$](img19.png) を
を 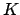 の関数として求めることが出来れば、
自由エネルギーを求めることが出来、従って種々の熱力学量
を求めることができる。
例えば、
の関数として求めることが出来れば、
自由エネルギーを求めることが出来、従って種々の熱力学量
を求めることができる。
例えば、
- 磁化
-
 |
(5) |
- 比熱
-
![\begin{displaymath}
C = \frac{T}{V} \frac{\partial S}{\partial T}
= - \frac{T}...
...{V} \left[
\langle E^2 \rangle - \langle E \rangle^2 \right]
\end{displaymath}](img25.png) |
(6) |
- 等温磁化率
-
![\begin{displaymath}
\chi_T = \frac{\partial M}{\partial H}
= - T \frac{1}{V} \...
...\left[ \langle \phi^2 \rangle - \langle \phi \rangle^2 \right]
\end{displaymath}](img26.png) |
(7) |
ここで、![$E=H[S]$](img27.png) は系のエネルギー、
は系のエネルギー、
 である。
である。
これらの熱力学関数に加えて、相関関数という量が重要である。
これは、系の自由度同士の相関が距離に従ってどのように変化
するかを表している。
![\begin{displaymath}
G(r\,; K) = \langle \phi_i \phi_{i+r} \rangle
= \frac{1}{Z} \mbox{Tr}\left[ \phi_i \phi_{i+r} e^{-\beta H[\phi;K]} \right]
\end{displaymath}](img29.png) |
(8) |
相関関数 が指数関数的に振る舞う場合、即ち
が指数関数的に振る舞う場合、即ち
 と書ける場合、
と書ける場合、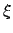 を相関距離と呼ぶ。
相関関数が指数関数的かどうかは、熱力学極限が取れるためには
重要である。
相関関数が巾乗的に振る舞う(
を相関距離と呼ぶ。
相関関数が指数関数的かどうかは、熱力学極限が取れるためには
重要である。
相関関数が巾乗的に振る舞う(
 )ような場合、
系の次元によっては、
熱力学極限で自由エネルギー密度が有限にならない場合がある。
)ような場合、
系の次元によっては、
熱力学極限で自由エネルギー密度が有限にならない場合がある。



Next: Ising モデル
Up: 統計物理と Ising モデル
Previous: 統計物理と Ising モデル
Hideo Matsufuru
2006-06-16
![]() で記述される系があるとする。
自由度を一般に
で記述される系があるとする。
自由度を一般に ![]() (i=1,2,...), 系のパラメターを
(i=1,2,...), 系のパラメターを ![]() (a=1,2,...)とする。
例えば、強磁性体の場合、
(a=1,2,...)とする。
例えば、強磁性体の場合、![]() としては各格子点上のスピン自由度、
Kはスピン間の結合定数や、外からかけた磁場
としては各格子点上のスピン自由度、
Kはスピン間の結合定数や、外からかけた磁場 ![]() などを表す。
などを表す。
![]() に関する統計
力学的平均値
に関する統計
力学的平均値
![]() は、アンサンブル平均、
は、アンサンブル平均、
![]() を
を ![]() の関数として求めることが出来れば、
自由エネルギーを求めることが出来、従って種々の熱力学量
を求めることができる。
例えば、
の関数として求めることが出来れば、
自由エネルギーを求めることが出来、従って種々の熱力学量
を求めることができる。
例えば、