


Next: Markov 過程
Up: Monte Carlo シミュレーション
Previous: Monte Carlo シミュレーション
一般に系の自由度  に対し Hamiltonian
に対し Hamiltonian 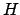 で記述
される系があるとする。
カノニカル・アンサンブルに対し、ある物理量
で記述
される系があるとする。
カノニカル・アンサンブルに対し、ある物理量 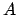 の期待値は、
次のように表される。
の期待値は、
次のように表される。
![\begin{displaymath}
\langle A \rangle = \frac{1}{Z} \sum_{\rm states}
A[\phi] e^{-\beta H[\phi]}
\end{displaymath}](img171.png) |
(55) |
ここで、 は系の自由度、
は系の自由度、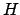 はその Hamiltonian、
はその Hamiltonian、
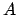 はある物理量とする。
和は、すべての状態について取る。
Ising モデルの場合には、
はある物理量とする。
和は、すべての状態について取る。
Ising モデルの場合には、 は 各格子点のスピン
は 各格子点のスピン  、
、
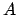 としては磁化や比熱、相関関数などとなる。
としては磁化や比熱、相関関数などとなる。
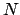 個のスピンからなるIsing系では、状態数は
個のスピンからなるIsing系では、状態数は 個となり、
個となり、
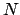 が小さい場合を除いて、すべての状態について実際に和を
評価することは現実的ではない。
が小さい場合を除いて、すべての状態について実際に和を
評価することは現実的ではない。
一方、上の式で、Boltzmann 因子
![$e^{-\beta H[\phi]}$](img173.png) は、
確率測度として解釈することができる。
この場合、系の配位
は、
確率測度として解釈することができる。
この場合、系の配位  をこのBoltzmann 因子
に等しい出現確率で生成することができれば、
その各配位に対して物理量
をこのBoltzmann 因子
に等しい出現確率で生成することができれば、
その各配位に対して物理量![$A[\phi]$](img175.png) を計算して平均することに
よって、
を計算して平均することに
よって、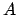 の統計力学的平均値
の統計力学的平均値
 を得ることが出来る。
即ち、
を得ることが出来る。
即ち、
![\begin{displaymath}
\langle A \rangle \simeq \frac{1}{N_{sample}}
\sum_i A[\phi_i]
\end{displaymath}](img176.png) |
(56) |
ここで  は、
は、
![$e^{-\beta H[\phi]}$](img173.png) の確率で
生成される、
の確率で
生成される、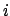 番目の場の配位である。
この方法では、
番目の場の配位である。
この方法では、
 への寄与が大きい配位、
つまり Boltzmannウェイトが大きい配位を集中的に
生成することによって、 効果的に計算を行なうことができる。
このような方法を、重点サンプリング(important sampling)
と呼んでいる。
への寄与が大きい配位、
つまり Boltzmannウェイトが大きい配位を集中的に
生成することによって、 効果的に計算を行なうことができる。
このような方法を、重点サンプリング(important sampling)
と呼んでいる。
Hideo Matsufuru
2006-06-16
![]() に対し Hamiltonian
に対し Hamiltonian ![]() で記述
される系があるとする。
カノニカル・アンサンブルに対し、ある物理量
で記述
される系があるとする。
カノニカル・アンサンブルに対し、ある物理量 ![]() の期待値は、
次のように表される。
の期待値は、
次のように表される。
![]() は、
確率測度として解釈することができる。
この場合、系の配位
は、
確率測度として解釈することができる。
この場合、系の配位 ![]() をこのBoltzmann 因子
に等しい出現確率で生成することができれば、
その各配位に対して物理量
をこのBoltzmann 因子
に等しい出現確率で生成することができれば、
その各配位に対して物理量![]() を計算して平均することに
よって、
を計算して平均することに
よって、![]() の統計力学的平均値
の統計力学的平均値
![]() を得ることが出来る。
即ち、
を得ることが出来る。
即ち、
![\begin{displaymath}
\langle A \rangle \simeq \frac{1}{N_{sample}}
\sum_i A[\phi_i]
\end{displaymath}](img176.png)