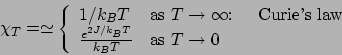Next: 2点相関関数
Up: 1次元 Ising モデル
Previous: 1次元 Ising モデル
1 次元 Ising モデルは、転送行列の方法を使って解くことができる。
( の場合には簡単に解く方法もあるが、重要な手法なので転送行列
を用いる。)
の場合には簡単に解く方法もあるが、重要な手法なので転送行列
を用いる。)
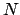 -自由度系を考え、周期的境界条件:
-自由度系を考え、周期的境界条件: 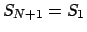 とする。
とする。
![\begin{displaymath}
Z_N(h,K) = \mbox{Tr}\exp\left[ h\sum_i S_i + K \sum_i S_i S_{i+1} \right]
\end{displaymath}](img60.png) |
(16) |
ここで、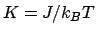 、
、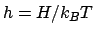 。
因子の積で表すと、
。
因子の積で表すと、
![\begin{displaymath}
Z_N(h,K) = \sum_{S_1} \sum_{S_2} \cdots \sum_{S_N}
[ e^{ \...
...S_2 S_3 } ] \cdots
[ e^{ \frac{h}{2}(S_N+S_1) + K S_N S_1 } ]
\end{displaymath}](img63.png) |
(17) |
ここで、それぞれの項を、行列の要素とみなす。
例えば、
![\begin{displaymath}
T_{S_1 S_2} = [ e^{ \frac{h}{2}(S_1+S_2) + K S_1 S_2 } ]
\end{displaymath}](img64.png) |
(18) |
即ち、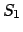 、
、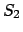 が次のような行列
が次のような行列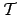 のラベルであると解釈する。
のラベルであると解釈する。
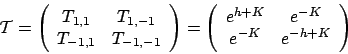 |
(19) |
このとき、
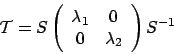 |
(20) |
と相似変換を行うことが出来る。
ここで、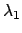 、
、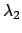 は、
は、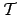 のふたつの
固有値とし、
のふたつの
固有値とし、
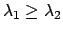 とする。
これらは容易に次のように求まる。
とする。
これらは容易に次のように求まる。
![\begin{displaymath}
\lambda_{1,2} = e^K \left[ \cosh(h) \pm \sqrt{ \sinh^2(h)+e^{-4K} }
\right]
\end{displaymath}](img73.png) |
(21) |
従って分配関数は、
これより、自由エネルギー密度は、
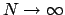 の極限で、
の極限で、
となる。
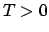 では、実の
では、実の 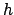 、
、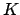 に対して
に対して 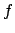 は解析的、
即ち相転移は存在しない。
非解析的になるのは、2乗根の中がゼロとなり、
は解析的、
即ち相転移は存在しない。
非解析的になるのは、2乗根の中がゼロとなり、
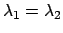 となる場合か、
となる場合か、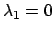 となる場合
であるが、これは、次の Perron の定理によって斥けられる。
となる場合
であるが、これは、次の Perron の定理によって斥けられる。
Perron-Frobenius の定理:
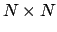 行列
行列 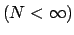
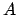 で
で 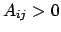 (for all
(for all 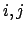 )
について、その最大の固有値は次の性質を持つ:
(a) 実、正定値、(b) 非縮退、(c)
)
について、その最大の固有値は次の性質を持つ:
(a) 実、正定値、(b) 非縮退、(c) 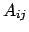 の解析的関数。
の解析的関数。
これによって、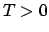 では相転移が起こらないことが結論づけられる。
これは、1次元の場合の特徴である。
1次元では転送行列は
では相転移が起こらないことが結論づけられる。
これは、1次元の場合の特徴である。
1次元では転送行列は 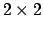 行列であったが、
2次元以上の場合には、転送行列は熱力学極限では
行列であったが、
2次元以上の場合には、転送行列は熱力学極限では
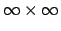 の行列となり、Perron-Frobenius の定理は適用できない。
の行列となり、Perron-Frobenius の定理は適用できない。
1次元で
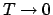 、従って
、従って
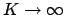 の場合を考える。
この時、
の場合を考える。
この時、
![$\lambda_1=e^K[\cosh(h)+\vert\sinh(h)\vert]=e^Ke^{\vert h\vert}$](img98.png) であるので、
であるので、
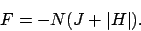 |
(26) |
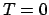 では、
では、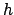 に対し、
に対し、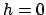 で
で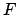 は非解析的。
磁化は、
は非解析的。
磁化は、
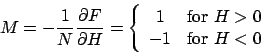 |
(27) |
まず、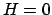 の場合。
このとき、自由エネルギーは、
の場合。
このとき、自由エネルギーは、
![\begin{displaymath}
F=-k_BTN[K+\log(1+e^{-2K})]
\end{displaymath}](img103.png) |
(28) |
内部エネルギー
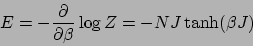 |
(29) |
比熱
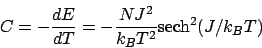 |
(30) |
磁化
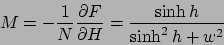 |
(31) |
とそれぞれなる。
ここで、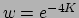 は、すべて上(あるいは下)向きのスピンの
配位に対して、ひとつのスピンだけがフリップした状態の
相対確率に対応する。
等温磁化率
は、すべて上(あるいは下)向きのスピンの
配位に対して、ひとつのスピンだけがフリップした状態の
相対確率に対応する。
等温磁化率 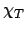 は次の式で定義される。
は次の式で定義される。
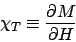 |
(32) |
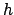 が小さい時、
が小さい時、
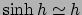 より、
より、
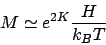 |
(33) |
この近似の時、磁化率 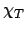 は、
は、
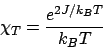 |
(34) |
高温と低温での極限では、
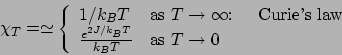 |
(35) |



Next: 2点相関関数
Up: 1次元 Ising モデル
Previous: 1次元 Ising モデル
Hideo Matsufuru
2006-06-16
![]() の場合には簡単に解く方法もあるが、重要な手法なので転送行列
を用いる。)
の場合には簡単に解く方法もあるが、重要な手法なので転送行列
を用いる。)
![]() -自由度系を考え、周期的境界条件:
-自由度系を考え、周期的境界条件: ![]() とする。
とする。
![\begin{displaymath}
Z_N(h,K) = \mbox{Tr}\exp\left[ h\sum_i S_i + K \sum_i S_i S_{i+1} \right]
\end{displaymath}](img60.png)
![\begin{displaymath}
Z_N(h,K) = \sum_{S_1} \sum_{S_2} \cdots \sum_{S_N}
[ e^{ \...
...S_2 S_3 } ] \cdots
[ e^{ \frac{h}{2}(S_N+S_1) + K S_N S_1 } ]
\end{displaymath}](img63.png)
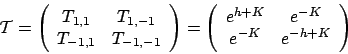
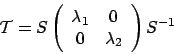
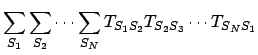
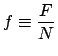
![$\displaystyle - \frac{k_BT}{N} \log Z_N[h,K]$](img80.png)
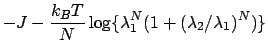
![$\displaystyle -J - k_BT \log\left[\cosh(h) + \sqrt{ \sinh^2(h)+e^{-4K}}
\right]$](img83.png)
![]() では、実の
では、実の ![]() 、
、![]() に対して
に対して ![]() は解析的、
即ち相転移は存在しない。
非解析的になるのは、2乗根の中がゼロとなり、
は解析的、
即ち相転移は存在しない。
非解析的になるのは、2乗根の中がゼロとなり、
![]() となる場合か、
となる場合か、![]() となる場合
であるが、これは、次の Perron の定理によって斥けられる。
となる場合
であるが、これは、次の Perron の定理によって斥けられる。
![]() 行列
行列 ![]()
![]() で
で ![]() (for all
(for all ![]() )
について、その最大の固有値は次の性質を持つ:
(a) 実、正定値、(b) 非縮退、(c)
)
について、その最大の固有値は次の性質を持つ:
(a) 実、正定値、(b) 非縮退、(c) ![]() の解析的関数。
の解析的関数。
![]() では相転移が起こらないことが結論づけられる。
これは、1次元の場合の特徴である。
1次元では転送行列は
では相転移が起こらないことが結論づけられる。
これは、1次元の場合の特徴である。
1次元では転送行列は ![]() 行列であったが、
2次元以上の場合には、転送行列は熱力学極限では
行列であったが、
2次元以上の場合には、転送行列は熱力学極限では
![]() の行列となり、Perron-Frobenius の定理は適用できない。
の行列となり、Perron-Frobenius の定理は適用できない。
![]() 、従って
、従って
![]() の場合を考える。
この時、
の場合を考える。
この時、
![]() であるので、
であるので、
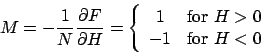
![]() の場合。
このとき、自由エネルギーは、
の場合。
このとき、自由エネルギーは、