


Next: 演習問題
Up: 1次元 Ising モデル
Previous: 転送行列
2点相関関数は次のように定義される。
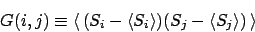 |
(36) |
転送行列の方法で求めるには、まず、
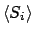 を次のように表す。
を次のように表す。
![\begin{displaymath}
\langle S_i \rangle
= \frac{1}{Z} \sum_{S_1}\sum_{S_2}\cdot...
..._2} \cdots T_{S_{i-1} S_i} S_i T_{S_i S_{i+1}}
\cdots \right]
\end{displaymath}](img115.png) |
(37) |
ここで、
![\begin{displaymath}
\sum_{S_i} T_{S_{i-1} S_i} S_i T_{S_i S_{i+1}}
= \left[ {\c...
...
= \left[ {\cal T} \sigma_z {\cal T} \right]_{S_{i-1}S_{i+1}}
\end{displaymath}](img116.png) |
(38) |
ここで 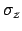 は Pauli 行列のz成分。
は Pauli 行列のz成分。
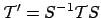 を対角行列とする相似変換を
を対角行列とする相似変換を
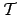 に対して行い、この変換行列
に対して行い、この変換行列 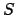 に対して
に対して
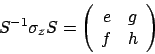 |
(39) |
とする。
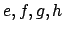 は
は 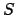 がTの固有ベクトルから構成されることから
あらわに計算出来る。
このとき、
がTの固有ベクトルから構成されることから
あらわに計算出来る。
このとき、
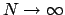 の熱力学的極限では、分子の第1項のみが寄与する。
の熱力学的極限では、分子の第1項のみが寄与する。
同様に、
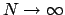 の熱力学的極限では、第1、2項のみが寄与し、
の熱力学的極限では、第1、2項のみが寄与し、
![$\displaystyle \langle S_i S_{i+j} \rangle - \langle S_i \rangle^2
= fg \left( \...
...t)^j
= fg \exp\left[ - j \log\left( \frac{\lambda_1}{\lambda_2}
\right) \right]$](img128.png) |
|
|
(44) |
これより、相関距離は
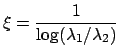 |
|
|
(45) |
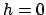 では
では
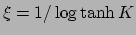 となる。
となる。
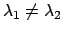 では、
では、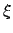 は発散しない。
一般に、転送行列の最大固有値が縮退しない限り、
は発散しない。
一般に、転送行列の最大固有値が縮退しない限り、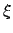 は発散しない。
は発散しない。
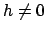 では、
では、
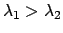 なので、この場合
相転移は無い。
なので、この場合
相転移は無い。
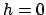 では、
では、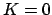 即ち
即ち 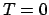 で
で
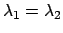 なので、
相転移が起こる。
なので、
相転移が起こる。



Next: 演習問題
Up: 1次元 Ising モデル
Previous: 転送行列
Hideo Matsufuru
2006-06-16
![\begin{displaymath}
\langle S_i \rangle
= \frac{1}{Z} \sum_{S_1}\sum_{S_2}\cdot...
..._2} \cdots T_{S_{i-1} S_i} S_i T_{S_i S_{i+1}}
\cdots \right]
\end{displaymath}](img115.png)
![\begin{displaymath}
\sum_{S_i} T_{S_{i-1} S_i} S_i T_{S_i S_{i+1}}
= \left[ {\c...
...
= \left[ {\cal T} \sigma_z {\cal T} \right]_{S_{i-1}S_{i+1}}
\end{displaymath}](img116.png)
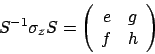
![$\displaystyle \frac{ \mbox{Tr}[ S^{-1}\sigma_z S ({\cal T}^N)] }{ \mbox{Tr}[({\cal T}^N)] }$](img123.png)
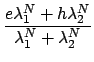
![$\displaystyle \frac{1}{Z} \mbox{Tr}\left[ (S^{-1}\sigma_z S) ({\cal T}')^j
(S^{-1}\sigma_z S) ({\cal T}')^{N-j}
\right]$](img126.png)
![$\displaystyle \frac{1}{Z} \mbox{Tr}(\lambda_1)^N \left[
e^2 + fg \left( \frac{\...
...\lambda_1} \right)^j
+ h^2 \left( \frac{\lambda_2}{\lambda_1} \right)^N
\right]$](img127.png)
![$\displaystyle \langle S_i S_{i+j} \rangle - \langle S_i \rangle^2
= fg \left( \...
...t)^j
= fg \exp\left[ - j \log\left( \frac{\lambda_1}{\lambda_2}
\right) \right]$](img128.png)
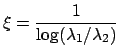
![]() では、
では、![]() は発散しない。
一般に、転送行列の最大固有値が縮退しない限り、
は発散しない。
一般に、転送行列の最大固有値が縮退しない限り、![]() は発散しない。
は発散しない。
![]() では、
では、
![]() なので、この場合
相転移は無い。
なので、この場合
相転移は無い。
![]() では、
では、![]() 即ち
即ち ![]() で
で
![]() なので、
相転移が起こる。
なので、
相転移が起こる。