Next: Bibliography
Up: 統計処理
Previous: 平均値と誤差
初めに、最も簡単なビン・サイズ1のジャックナイフ法を説明する。
まず、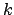 番目のデータを除いた統計平均を定義する。
番目のデータを除いた統計平均を定義する。
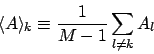 |
(81) |
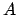 の関数である物理量を
の関数である物理量を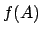 とすると、
とすると、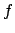 の平均値とその誤差は、
次のように計算される。
の平均値とその誤差は、
次のように計算される。
これらの定義を、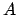 に適用すれば、
Eqs. (78), (79) になることが
容易に確認できる。
に適用すれば、
Eqs. (78), (79) になることが
容易に確認できる。
同様にして、ビン・サイズ m のジャックナイフ法は次のような
手順となる。
まず全データを、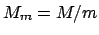 個のビンに分割する。
それぞれのビンには、
個のビンに分割する。
それぞれのビンには、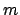 個のデータがあることになる。
各ビンにラベル
個のデータがあることになる。
各ビンにラベル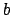 (
(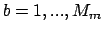 )を割り当て、このビンの
要素の集合を
)を割り当て、このビンの
要素の集合を 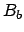 で表す。
ビン
で表す。
ビン 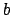 のデータを取り除いた平均値を、
のデータを取り除いた平均値を、
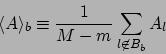 |
(84) |
これを用いて、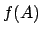 の平均値と誤差は、次のようになる。
の平均値と誤差は、次のようになる。
ジャックナイフ法の特長は次の通りである。
- 任意の物理量
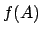 に対して誤差が計算できる。
に対して誤差が計算できる。
- 磁化率や比熱のような、分散に関係した物理量の誤差を
求めることができる。
- 物理量の間の相関を取り入れた誤差評価になっている。
例えば、相関距離を
![$\log[G(j)/G(j+1)]$](img256.png) によってラフに評価する
場合を考える。
この時、
によってラフに評価する
場合を考える。
この時、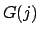 と
と 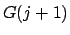 は強く相関しているため、誤差の伝播則では
正しく評価できない。
ジャックナイフ法によると、この相関まで含めた誤差の評価になっている。
は強く相関しているため、誤差の伝播則では
正しく評価できない。
ジャックナイフ法によると、この相関まで含めた誤差の評価になっている。
- ビン・サイズを大きくして行くことによって、測定を行った
配位の間の相関(自己相関、autocorrelaton)を評価できる。
これは、相関が無い場合には、ジャックナイフ法で評価した誤差は
ビン・サイズに寄らないため、誤差のビン・サイズに対する依存性
をみることによって、相関がどれくらいのステップ数残っているかを
見積もることが出来るということである。
一方で、ジャックナイフ法では、通常の誤差評価
Eqs. (78), (79) と同じく、
誤差は平均値に対してプラスマイナスに対称な評価である。
平均値に対し誤差が十分小さくない場合、プラス方向の誤差と
マイナス方向の誤差は一般に異なるが、このような場合は
ジャックナイフ法では正しく評価できない。
そのような場合には、ブートストラップ法などの、
より複雑な評価を行う必要がある。
Hideo Matsufuru
2006-06-16
![]() 番目のデータを除いた統計平均を定義する。
番目のデータを除いた統計平均を定義する。
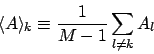
![]() 個のビンに分割する。
それぞれのビンには、
個のビンに分割する。
それぞれのビンには、![]() 個のデータがあることになる。
各ビンにラベル
個のデータがあることになる。
各ビンにラベル![]() (
(![]() )を割り当て、このビンの
要素の集合を
)を割り当て、このビンの
要素の集合を ![]() で表す。
ビン
で表す。
ビン ![]() のデータを取り除いた平均値を、
のデータを取り除いた平均値を、