Next: ジャックナイフ法
Up: 統計処理
Previous: 統計処理
この節の記述は、文献[4]に従っている。
独立な測定データ 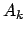 (
(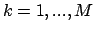 )に対する
平均値とその誤差は、次の式で与えられる。
)に対する
平均値とその誤差は、次の式で与えられる。
いくつかの物理量 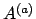 の関数として表される量
の関数として表される量
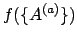 の誤差を見積もるためには、次の誤差の伝播則を用いる。
の誤差を見積もるためには、次の誤差の伝播則を用いる。
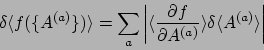 |
(80) |
しかしながら、複雑な関数 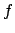 に対して誤差の伝播則を適用すると、
誤差を過大に見積もる場合が多い。
また、比熱や磁化率のような、分散が物理量となる場合、
Eq. (79)によって誤差を見積もるのは簡単ではない。
そのような場合には、次のジャックナイフ法を用いるのが便利である。
に対して誤差の伝播則を適用すると、
誤差を過大に見積もる場合が多い。
また、比熱や磁化率のような、分散が物理量となる場合、
Eq. (79)によって誤差を見積もるのは簡単ではない。
そのような場合には、次のジャックナイフ法を用いるのが便利である。
Hideo Matsufuru
2006-06-16
![]() (
(![]() )に対する
平均値とその誤差は、次の式で与えられる。
)に対する
平均値とその誤差は、次の式で与えられる。