
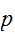 にしたがって出現するとみなすとき、これを確率変数といい
にしたがって出現するとみなすとき、これを確率変数といい

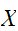 ,
,
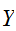 ,
,
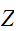 などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と身長、体重などのように取り得る値の範囲を持った連続型とがある。
などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と身長、体重などのように取り得る値の範囲を持った連続型とがある。
総研大・KEK夏期実習:数値シミュレーション入門 --Ising Model のMonte Calro シミュレーション --
柴田章博、松古栄夫
2008年6月2日-4日
「数値シミュレーション入門」は、確率的計算技法としてとしてモンテカルロ法に基づくシミュレーションの入門の実習を行う。モンテカルロ法は物理学においてはメトロポーリスらによって流体シミュレーションの方法として提唱され、統計物理学など様々な分野応用されるようになった。統計力学に基づくモンテカルロシミュレーションの手法の基礎を紹介する。磁性体の統計力学のモデルは、本来の磁性体の性質を解明のみならず、さまざまな広範な問題に応用されている。物性物理学やのや物理化学のシミュレーションや素粒子物理学の格子ゲージ理論シミュレーションののみならず、統計的手法に基づく情報処理の分野やニューラルネットワークの学習理論などさまざまである。
本実習は、モンテカルロ積分の基本的なアイデアから出発して、統計力学の基本的なモデルあるイジングモデル(Ising model)を題材にその統計物理学的な解析的法(解析的び数値的方法(数値シミュレーションの方法))を解説する。また、実際にシミュレーションをおこないさまざまな量を測ることによって数値シミュレーションの手法を体得することを目的とする。
ある変数のとる値が事前に予知されず確率
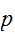 にしたがって出現するとみなすとき、これを確率変数といい
にしたがって出現するとみなすとき、これを確率変数といい

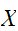 ,
,
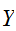 ,
,
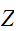 などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と身長、体重などのように取り得る値の範囲を持った連続型とがある。
などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と身長、体重などのように取り得る値の範囲を持った連続型とがある。
確率分布は、ある変数がどの値をとる可能性が大きいか、小さいかを実現値と確率の間の関数として現したものである(通常

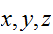 などの小文字で表現する)。ある変数が
などの小文字で表現する)。ある変数が

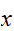 以下である確率を知りたいとき、
以下である確率を知りたいとき、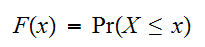 と現す。この関数はある
と現す。この関数はある
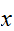 を与えるとこめられることであり、累積分布関数(単に分布関数)と呼ばれる。この関数は単調非減少関数で、有限の値を仮定して次のようのにとる。
を与えるとこめられることであり、累積分布関数(単に分布関数)と呼ばれる。この関数は単調非減少関数で、有限の値を仮定して次のようのにとる。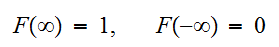 分布関数は、微分可能な場合が多く、その導関数を確率密度関数と呼び、
分布関数は、微分可能な場合が多く、その導関数を確率密度関数と呼び、
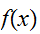 と書くことにする。
と書くことにする。
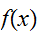 はすべての
はすべての
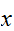 に対して、
に対して、
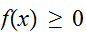 であり、
であり、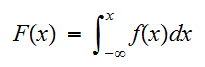 と現される。特に、
と現される。特に、
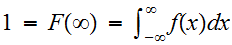 である。また、
である。また、
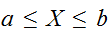 である確率は、
である確率は、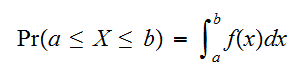 とあらわせる。連続変数の場合、一点の積分はゼロであるので、
とあらわせる。連続変数の場合、一点の積分はゼロであるので、
 である。
である。
一方、離散変数である場合には、
 であって、分布関数は積分記号でなく、和記号で現される。
であって、分布関数は積分記号でなく、和記号で現される。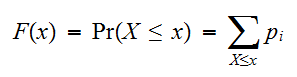
確率変数の分布の様子を示す指標として、分布の中心やバラつきの度合いを示す指標があると便利である。分布の中心を現すものとして、代表的なのが期待値と分散である。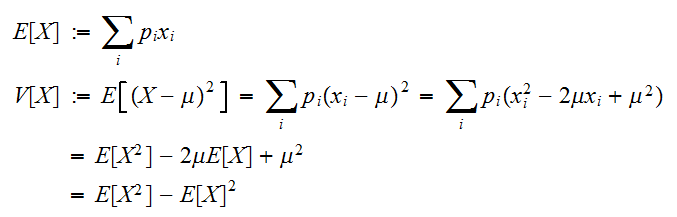 たたし、
たたし、
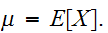 一方、連続変数に対して次で与えられる。
一方、連続変数に対して次で与えられる。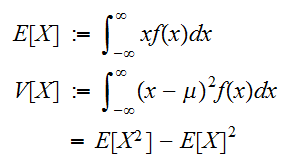
連続型確率変数
 が区間
が区間
![$[a,b]$](graphics/text1__25.png) 間で確率密度一定である分布を連続型一様分布(Unifoem
distribution)といい、
間で確率密度一定である分布を連続型一様分布(Unifoem
distribution)といい、
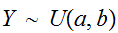 と略記する。これは、確率密度
と略記する。これは、確率密度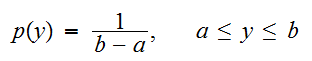 で与えられる。
で与えられる。
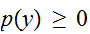 、かつ
、かつ
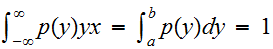 である。
である。
一様分布の平均、分散は次で与えられる。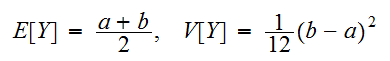
正規分布(nomal
distribuytion)は次のように与えられ、
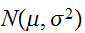 で略記する。
で略記する。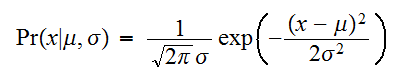 特に、
特に、
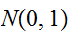 のものを標準正規分布(図normDist)とよび、この分布に従う確率変数は、
しばしば
のものを標準正規分布(図normDist)とよび、この分布に従う確率変数は、
しばしば
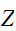 と関数
と関数
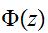 を用いて現される。
を用いて現される。
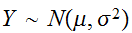 と
と

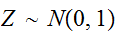 は、
は、
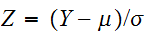 の関係でいつでも変換することができる。正規分布の平均、分散は次で与えられる。
の関係でいつでも変換することができる。正規分布の平均、分散は次で与えられる。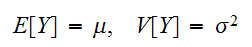
連続型確率変数の組
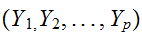 について分布を考える。それぞれの区間
について分布を考える。それぞれの区間
![$(a_{1},b_{1}]$](graphics/text1__41.png) 、
、
![$(a_{2},b_{2}]$](graphics/text1__42.png) に変数が同時に入る同時確率は、同時確率密度関数
に変数が同時に入る同時確率は、同時確率密度関数 
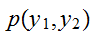 をもちいて
をもちいて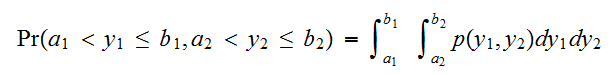 で与えられる。
で与えられる。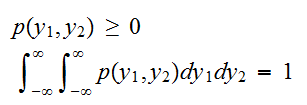 を満たさなければならない。
を満たさなければならない。
 の周辺分布は次のように得られる。
の周辺分布は次のように得られる。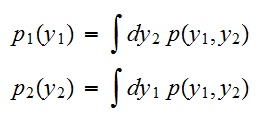 このように、積分によって変数を消去することを周辺化という。
このように、積分によって変数を消去することを周辺化という。

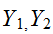 の同時確率密度(同時分布)
の同時確率密度(同時分布)
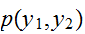 が与えられたとき
が与えられたとき
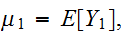

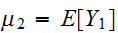 とするとき
とするとき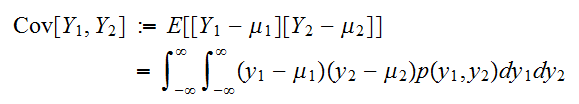 は,
は,
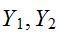 の共分散とよぶ。また、
の共分散とよぶ。また、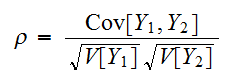 は相関関数と呼ばれる(
は相関関数と呼ばれる(
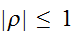 )。この量は、しばし
)。この量は、しばし
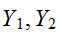 との間の線形相関関係の強さを示す量と解釈される。相関係数が最大(最小)の
との間の線形相関関係の強さを示す量と解釈される。相関係数が最大(最小)の
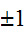 をとる場合は、
をとる場合は、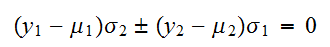 ときである。言い換えると、すべてのデータが直線(eq:line)上にあるときである。
ときである。言い換えると、すべてのデータが直線(eq:line)上にあるときである。
一方、
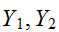 とが独立ならば、必ず
とが独立ならば、必ず
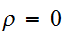 となる。実際、
となる。実際、 
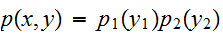 の時、
の時、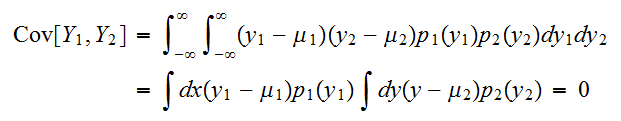 である。しかし、逆に
である。しかし、逆に
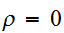 であっても必ずしも、
であっても必ずしも、
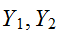 は独立とは限らない。たとえば、半径1の円周上に点が分布する場合
は独立とは限らない。たとえば、半径1の円周上に点が分布する場合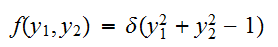 (ここで
(ここで
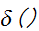 はディラックのデルタ関数)には、
はディラックのデルタ関数)には、
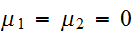 ,
,
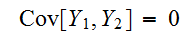 であるが、
であるが、
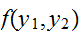 は独立分布ではない。
は独立分布ではない。
統計処理においては、ランダムな誤差を含んだ測定値や観測量の集計を行う。その基本的な、操作である確率の変数の和
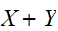 についてその性質を調べる。期待値については、加法性が成立する。
についてその性質を調べる。期待値については、加法性が成立する。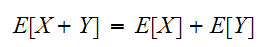 さらに
さらに
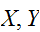 が独立であるときは、分散の加法性が成立する。
が独立であるときは、分散の加法性が成立する。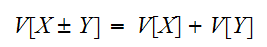

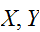 が独立でない時は、
が独立でない時は、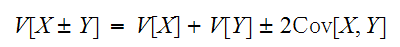 である。分散の加法性が成立するためには、無相関であれば十分となる。
である。分散の加法性が成立するためには、無相関であれば十分となる。
n個の変数
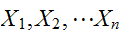 にたいして期待値の加法性が成立する。
にたいして期待値の加法性が成立する。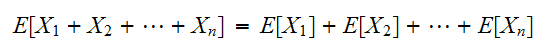 また、
また、
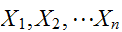 が独立な場合には、分散の加法性が成立する。
が独立な場合には、分散の加法性が成立する。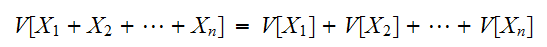
いま、n個の変数
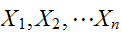 が同一分布に従うとき、これらの期待値、分散を
が同一分布に従うとき、これらの期待値、分散を
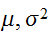 であるとすれば、
であるとすれば、
![$E[X_{k}]=\mu $](graphics/text1__82.png) ,
,
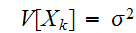 ,
,
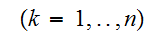 であるので
であるので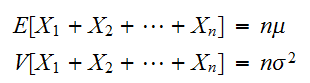 である。したがって標準偏差は、
である。したがって標準偏差は、
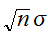 と
と
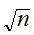 に比例することが重要である。
に比例することが重要である。
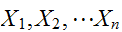 の相加平均
の相加平均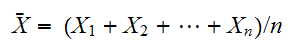 とおくと相加平均の期待値、分散は次で与えられる。
とおくと相加平均の期待値、分散は次で与えられる。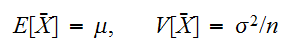
確率変数

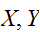 が独立で、それぞれ
が独立で、それぞれ
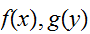 に従うとすると、和
に従うとすると、和

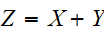 の従う確率分布
の従う確率分布
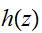 を考える。
を考える。
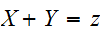 となるのは、
となるのは、
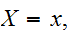

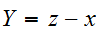 の同時分布のすべての和であるから、離散分布のとき
の同時分布のすべての和であるから、離散分布のとき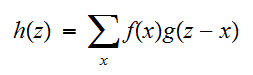 であり、連続分布のときは、和を積分に置き換えればよく
であり、連続分布のときは、和を積分に置き換えればよく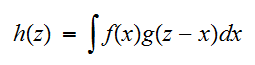 となる。関数
となる。関数
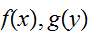 から、
から、
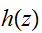 をつくる操作を畳み込みという。
をつくる操作を畳み込みという。
たとえば、
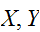 が正規分布
が正規分布
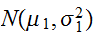 、
、
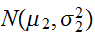 に従うとき、その畳み込み(記号
に従うとき、その畳み込み(記号

 を使って表現する)は、
を使って表現する)は、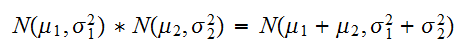 となる。すなわち、
となる。すなわち、
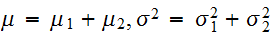 の正規分布になる。
の正規分布になる。
多変数
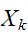 がそれぞれ
がそれぞれ
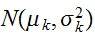 (
(
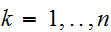 )であるとき、
)であるとき、
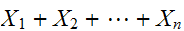 は
は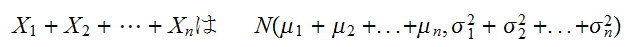 に従う。とくに
に従う。とくに
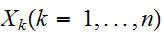 が同一分布
が同一分布
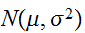 に従うとき、
に従うとき、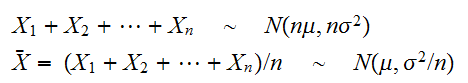 にそれぞれ従う。
にそれぞれ従う。
いま、
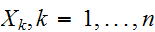 が互いに無相関で期待値
が互いに無相関で期待値
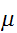 、分散
、分散
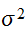 であるとすると、
であるとすると、
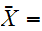

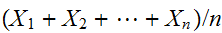 にたいして、
にたいして、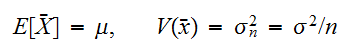 が成り立つ。このときチェビシェフの不等式
が成り立つ。このときチェビシェフの不等式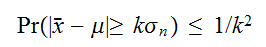 を適用すると、
を適用すると、
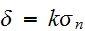 に対して
に対して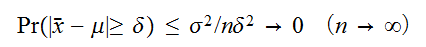 が成立する。ここで、
が成立する。ここで、
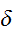 がどんなに小さな正定数であっても、十分大きな
がどんなに小さな正定数であっても、十分大きな
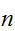 をとることで、式(eq:LargeNth)の右辺はいくらでも小さくすることができる。すなわち、
をとることで、式(eq:LargeNth)の右辺はいくらでも小さくすることができる。すなわち、
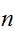 を大きくとることで、
を大きくとることで、
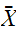 が
が
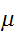 の近辺に集中していることが2次の積率(moment)までの確率でいえる。この事実を大数の弱法則(大数の法則)という。標語的にいえば、「大標本では観察された標本平均を母集団の真の平均とみなしてよい。」となる。
の近辺に集中していることが2次の積率(moment)までの確率でいえる。この事実を大数の弱法則(大数の法則)という。標語的にいえば、「大標本では観察された標本平均を母集団の真の平均とみなしてよい。」となる。

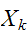 ,
,
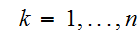 が互いに独立かつ同一の確率分布に従う確率変数列で、
が互いに独立かつ同一の確率分布に従う確率変数列で、
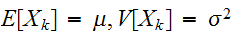 とする。このとき、
とする。このとき、
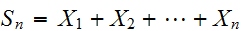 にたいして、つぎが成立する。
にたいして、つぎが成立する。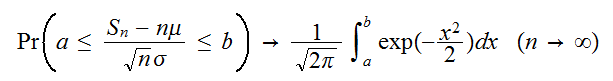 すなわち、
すなわち、
 は常に正規分布に近づいていくことが知られている。(証明略)。これを中心極限定理と呼ぶ。標語的にいえば「和
は常に正規分布に近づいていくことが知られている。(証明略)。これを中心極限定理と呼ぶ。標語的にいえば「和
 は
は
 が十分大きければ、大体正規分布であると考えてよい。」となる。
が十分大きければ、大体正規分布であると考えてよい。」となる。
モンテカルロ法 Note_1 というと乱数を使った円周率
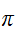 の計算の例を聞いたことがあるかもしれない。統計物理学に基づくモンテカルロシミュレーションは、必ずしも単純な積分を意味しないが、モンテカルロ技法の一端を見ることができるるので、モンテカルロ積分について概観する。
の計算の例を聞いたことがあるかもしれない。統計物理学に基づくモンテカルロシミュレーションは、必ずしも単純な積分を意味しないが、モンテカルロ技法の一端を見ることができるるので、モンテカルロ積分について概観する。
実際の円周率の計算には、計算誤差が大きくモンテカルロ法が用いられることはないが。しかし高次元の数値積分においては、計算手続きが指数的に増大し、積分区間を
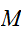 点に分割する
点に分割する
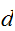 -次元の積分公式を使うと計算量が
-次元の積分公式を使うと計算量が
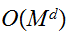 のオーダになる。非常に自由度の大きな積分を実行するには、一般に計算量が積分の次元に依存しないモンテカルロ法が有利となる。
のオーダになる。非常に自由度の大きな積分を実行するには、一般に計算量が積分の次元に依存しないモンテカルロ法が有利となる。
最も簡単な例を考える。積分領域
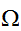 と、関数値域
と、関数値域
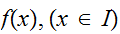 を囲む領域
を囲む領域
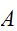 を考え、領域
を考え、領域
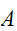 にランダムな点を振る。
にランダムな点を振る。
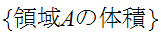 が分かっているとすれば、曲線
が分かっているとすれば、曲線
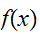 の下側の領域の体積は、生成したランダムな点が曲線
の下側の領域の体積は、生成したランダムな点が曲線
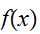 の下側の領域に含まれる割合として計算できる。すなわち、
の下側の領域に含まれる割合として計算できる。すなわち、
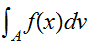 が次のように計算される。
が次のように計算される。
 この方法は、曲面(曲線)
この方法は、曲面(曲線)
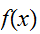 が複雑な形状をしていても、曲線
が複雑な形状をしていても、曲線
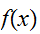 の下側の領域の点の生成と積分を容易に行うことが出来る利点がある。しかし、一般に効率のよい方法ではなく、見積もりの誤差も議論されなければならない。
の下側の領域の点の生成と積分を容易に行うことが出来る利点がある。しかし、一般に効率のよい方法ではなく、見積もりの誤差も議論されなければならない。

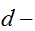 次元空間の領域領域
次元空間の領域領域
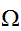 (体積
(体積
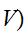 の変数
の変数
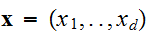 の関数
の関数

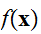 の多重積分
の多重積分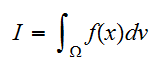 を求めることを考える。モンテカルロ積分(一様サンプリング法)では、積分領域
を求めることを考える。モンテカルロ積分(一様サンプリング法)では、積分領域
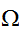 から一様ランダムに抽出した
から一様ランダムに抽出した
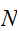 個の点
個の点
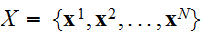 を使って積分値を推定する。(さいころを振って積分する。)代表点
を使って積分値を推定する。(さいころを振って積分する。)代表点
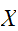 の大きな
の大きな
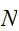 の極限で近似値
の極限で近似値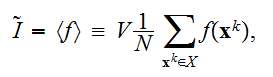 は、大数の法則によって、積分
は、大数の法則によって、積分
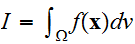 に収束する。ここで、角括弧は、
に収束する。ここで、角括弧は、
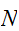 個の点における算術平均を意味する。一様ランダムサンプリング(同一分布)に対する、相加平均の期待値、分散は式(eq:EV-Ensamble)で与えられるから、
個の点における算術平均を意味する。一様ランダムサンプリング(同一分布)に対する、相加平均の期待値、分散は式(eq:EV-Ensamble)で与えられるから、
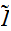 の見積もりの誤差は
の見積もりの誤差は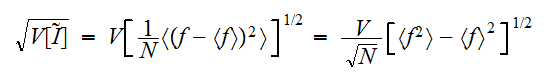 となる。台形公式における誤差オーダーは
となる。台形公式における誤差オーダーは

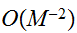 であるのに対し、モンテカルロ法の誤差の見積もりは
であるのに対し、モンテカルロ法の誤差の見積もりは

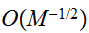 であり、とても悪く思われる。しかしながら、積分区間を
であり、とても悪く思われる。しかしながら、積分区間を
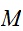 点に分割する
点に分割する
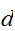 -次元の積分公式を使うと計算量が
-次元の積分公式を使うと計算量が
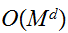 のオーダであるため、積分公式に基づく積分値の推定には高次元ではべき級数的に増大する。一方で、モンテカルロ法では
のオーダであるため、積分公式に基づく積分値の推定には高次元ではべき級数的に増大する。一方で、モンテカルロ法では
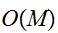 の計算量となる。
の計算量となる。
実際の計算を行う際には、与えられた領域
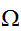 の一様サンプリングされた点と体積
の一様サンプリングされた点と体積
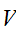 がわかっていることが前提となるが、実際の計算できるのは
がわかっていることが前提となるが、実際の計算できるのは
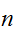 次元直方体の領域など限られた場合である。
次元直方体の領域など限られた場合である。
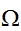 が複雑な形状を持った領域の場合は、体積の見積もり及び一様サンプリングか容易に行える
が複雑な形状を持った領域の場合は、体積の見積もり及び一様サンプリングか容易に行える
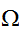 を囲む領域
を囲む領域
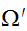 を導入することで、
を導入することで、
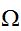 内の点を生成することが可能である。また、領域
内の点を生成することが可能である。また、領域
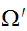 (体積
(体積
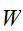 )で定義された関数
)で定義された関数
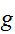 を
を
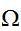 内の点
内の点
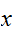 に対して、
に対して、
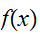 、外の点においてゼロであるように定義すれば
、外の点においてゼロであるように定義すれば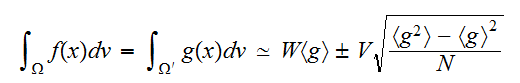 として積分を推定することができる。
として積分を推定することができる。
一様サンプリングによるモンテカルロ積分は次のような問題点がある。高次元空間の中の一様のサンプリングを生成することは難しい。一様にサンプリングポイントが生成できたとしても、被積分関数の評価値がほとんどの点で小さく結果的に無駄な計算となり、評価誤差が大きくなってしまう。
このような状況を改善するために積分を次のようにある確率分布関数

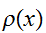 を用いて書き換えることを考える Note_2 :
を用いて書き換えることを考える Note_2 :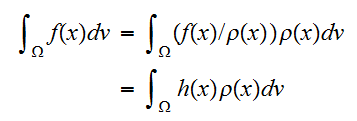 ここで、
ここで、
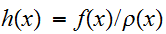 とおいた。
いま一様な重み
とおいた。
いま一様な重み

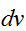 でサンプリングする代わりに、重み
でサンプリングする代わりに、重み
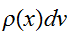 でサンプリングができるとしたらどうなるであろうか。このようサンプルされた点は、確率分布
でサンプリングができるとしたらどうなるであろうか。このようサンプルされた点は、確率分布
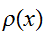 で点が生成することに対応する。
で点が生成することに対応する。
相加平均の期待値、分散の式(eq:EV-Ensamble)によれば、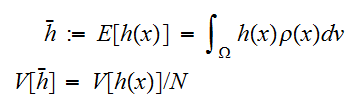 であるから、積分
であるから、積分
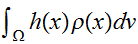 の値とその誤差は、関数
の値とその誤差は、関数
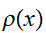 に従うサンプリング点
に従うサンプリング点
 で関数の値
で関数の値
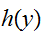 の期待値と分散で与えられる。
の期待値と分散で与えられる。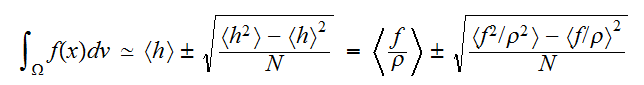 一様サンプリングの場合は、
一様サンプリングの場合は、
 一定
一定
 の場合である。
の場合である。
この式は
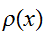 の選び方によらないことに注意。したがって、一様サンプリング法を改善するためには、
の選び方によらないことに注意。したがって、一様サンプリング法を改善するためには、
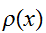 をうまく選んで積分に寄与するところを重点的にサンプルすればよいように思われる。
をうまく選んで積分に寄与するところを重点的にサンプルすればよいように思われる。
では、もっとも効率のよい
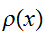 の選び方は何であろうか。それは、積分の推定誤差
の選び方は何であろうか。それは、積分の推定誤差
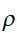 が与えられた
が与えられた
 にたいして最小となるように選べばよい。すなわち、拘束条件(eq:ProbCond)をみたし、
にたいして最小となるように選べばよい。すなわち、拘束条件(eq:ProbCond)をみたし、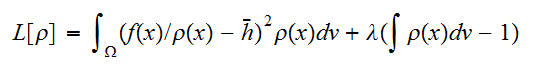 が最小になるような
が最小になるような
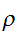 を求る変分問題
を求る変分問題
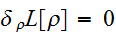 をとけばよい。これを解くと
をとけばよい。これを解くと
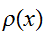 は次の最適解
は次の最適解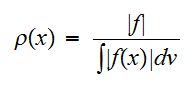 を満たせば良い。
を満たせば良い。
実際には、重点サンプリングでモンテカルロ積分を行うには、
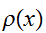 の分布を与えるアルゴリズムを構築しなければならないが、一般の関数
の分布を与えるアルゴリズムを構築しなければならないが、一般の関数
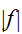 に対して構成することはできない。この節では、一般の
に対して構成することはできない。この節では、一般の
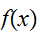 に対する重点サンプリングのアルゴリズムについては触れることはしない。重点サンプリング法を拡張した、適応型モンテカルロ積分の方法として、VEGASアルゴリズムが知られている。(たとえば、Numerical
Recipies in C/C++ NRinC/C++
を参照)。
に対する重点サンプリングのアルゴリズムについては触れることはしない。重点サンプリング法を拡張した、適応型モンテカルロ積分の方法として、VEGASアルゴリズムが知られている。(たとえば、Numerical
Recipies in C/C++ NRinC/C++
を参照)。
本実習で扱う統計力学に基づくのモンテカルロシミュレーションが、多次元の重点サンプリングの分布関数を生成するアルゴリズムを与えるあたること、さまざまな物理量を測ることが重点サンプリングによる多次元積分を実行することに対応することをみる。
Donald E. Knuth, "The art of Computer Programing" Vo2. Seminumerical Alogorithm. Addidon-Wesly, 2nd edition 1981. (サイエンス社からの邦訳あり)
奥村晴彦 「C言語によるアルゴリズム事典」 技術評論社ISBM4-87408-414-1
伏見正則「乱数」東京大学出版,1989
G.E.P. Box amd M.E. Muller, An. math. Statist. 26: 610 (1958); G.Mardagla and T.A.Bray, Rev. Soc. Ind. Appl. Math. 6 260(1964)
Numerical Recipies in C/C++ the art of Scientific Computing 2nd edition, W.H. Press 他著、Cambridge Press
統計的情報処理と統計力学, 田中和之編著, 臨時別冊・数理科学 SCGライブラリ50