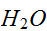 )が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。
)が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。
総研大・KEK夏期実習 --数値シミュレーション入門- 統計力学と情報処理
柴田章博松古栄夫 KEK計算化学センター
2006年6月13-15日
多数の要素が互いに影響を及ぼしあっている(相互作用している)とき、どのようなマクロな性質を持つかを解明するのが統計力学の重要な課題である。たとえば、水(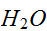 )が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。
)が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。
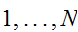 までの番号づけれれた格子点(site)に,値を持つ場を考えよう。格子点は、結晶の原子の配置でもよいし、(白黒)画像のピクセルやニューロン(神経細胞)でもよい。ここでは、
までの番号づけれれた格子点(site)に,値を持つ場を考えよう。格子点は、結晶の原子の配置でもよいし、(白黒)画像のピクセルやニューロン(神経細胞)でもよい。ここでは、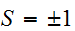 の2値を持つ、Ising
スピン(spin)を対応させたモデルを考えることにする。磁性体のモデルでは、
の2値を持つ、Ising
スピン(spin)を対応させたモデルを考えることにする。磁性体のモデルでは、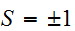 は、原子レベルの磁石(のNSの向き)が、上下のいずれを向いているかをあらわしている。いま、お互いに隣り合ったサイト同士
は、原子レベルの磁石(のNSの向き)が、上下のいずれを向いているかをあらわしている。いま、お互いに隣り合ったサイト同士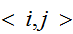 が相互作用するとして、相互作用のエネルギーとして、
が相互作用するとして、相互作用のエネルギーとして、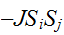 を考える。
を考える。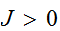 の時、
の時、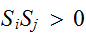 のとき、スピンが揃うときがエネルギーが低くなり安定である。一方、
のとき、スピンが揃うときがエネルギーが低くなり安定である。一方、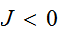 のときは、
のときは、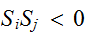 のとき、スピンがお互い反対向きのときが、安定となる。また、磁性体のときにおける外部磁場
のとき、スピンがお互い反対向きのときが、安定となる。また、磁性体のときにおける外部磁場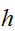 との相互作用
との相互作用
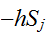 を付け加えた系を考える。統計力学では、系全体のエネルギー取り扱うハミルトンの関数(ハミルトニアン)を用いて系を記述する。
を付け加えた系を考える。統計力学では、系全体のエネルギー取り扱うハミルトンの関数(ハミルトニアン)を用いて系を記述する。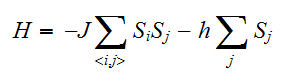 Isingモデルにおいては、系の相互作用は最近接相互作用でその強さが共通であるが、相互作用の形がどのようになるかは問題によって異なることを注意しておく。
Isingモデルにおいては、系の相互作用は最近接相互作用でその強さが共通であるが、相互作用の形がどのようになるかは問題によって異なることを注意しておく。
統計力学の処方箋(詳しくは、統計力学とIisngモデルで解説)によると、ハミルトニアンが与えられると、スピンがとる配位の確率分布は、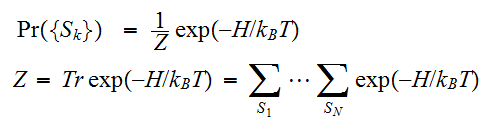 で与えられる。ここで
で与えられる。ここで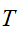 は温度、
は温度、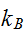 はボルツマン(Boltzmann)
の定数である。
はボルツマン(Boltzmann)
の定数である。
Isingモデルの統計力学の解析の例として画像修復の問題を紹介する。雑音によって乱れた不完全な画像が与えられたとき現画像を推定する問題は、ベイズの公式を用いて、確率論を用いた画像修復の問題として定式化され、統計力学のシミュレーションの手法を応用することができることをみる。
2次元の白黒の画像を考えると、各ピクセルは、格子点上のイジングスピン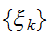 と対応付けることができる。元の画像
と対応付けることができる。元の画像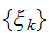 は、受信側では
は、受信側では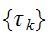 で表現されるとする。画像は、伝送の間に乱され確率
で表現されるとする。画像は、伝送の間に乱され確率 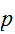 で、ビットが反転すると、
で、ビットが反転すると、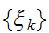 が与えられたときの
が与えられたときの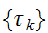 の出現確率は次で与えられる。
の出現確率は次で与えられる。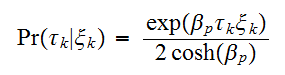 各サイトでビット反転が独立であるとすると、全体では、
各サイトでビット反転が独立であるとすると、全体では、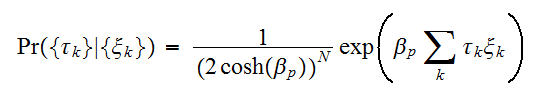 である。画像修復では、劣化画像
である。画像修復では、劣化画像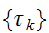 から、原画
から、原画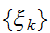 を推定するもんだいであるので、推定画像を
を推定するもんだいであるので、推定画像を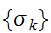 と書くとすると、ベイズの公式
と書くとすると、ベイズの公式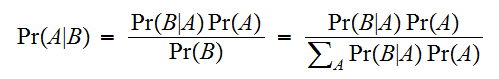 を用いて次のようにかける。
を用いて次のようにかける。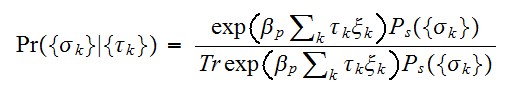 これは、劣化画像
これは、劣化画像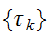 及び、事前知識
及び、事前知識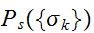 が画像修復に必要であることを示している。ここでは、
が画像修復に必要であることを示している。ここでは、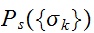 が正確にわからなくても、モデル分布
が正確にわからなくても、モデル分布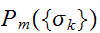 を
を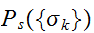 の代わりに使うこととする。
の代わりに使うこととする。
モデル分布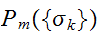 を次のように構成する:
を次のように構成する:
白の背景の中に孤立した黒の点がある場合は、もともとあった黒であるよりも、白の点がノイズによって反転した可能性が大きいと考える。このことを、隣り合うピクセル対は、違う状態であるよりもおなっ状態である確率が高いと解釈し、次の事前分布のモデルを導入する。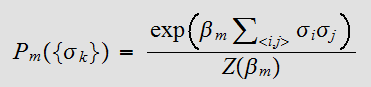 ここで、
ここで、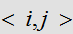 は隣同士のピクセルについての和であり、
は隣同士のピクセルについての和であり、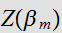 は企画化因子である。
は企画化因子である。
これはイジングモデルをあらわす。したがって、式(eq:BaysePix)へ事前分布を代入すると、画像修復の確率分布(事後分布)は、イジング模型にランダムな磁場がかかったスピン系の統計力学の問題となった。
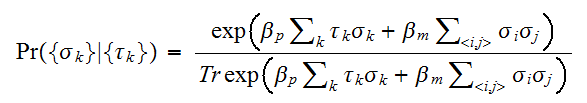 最大事後確率の考え方に立てば、式(eq:MAPPiX)を最大にする
最大事後確率の考え方に立てば、式(eq:MAPPiX)を最大にする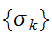 が修復画像となる。
が修復画像となる。