
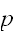 にしたがって出現するとみなすとき、これを確率変数といい
にしたがって出現するとみなすとき、これを確率変数といい

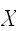 ,
,
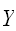 ,
,
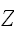 などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と体重などの値の範囲を持った連続型がある。
などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と体重などの値の範囲を持った連続型がある。
総研大・KEK夏期実習:数値シミュレーション入門 --Ising Model のMonte Calro シミュレーション --
柴田章博、松古栄夫
2006年6月13日-15日
「数値シミュレーション入門」は統計力学に基づくモンテカルロシミュレーションの手法の基礎を紹介する。磁性体の統計力学のモデルは、本来の磁性体の性質を解明のみならず、さまざまな広範な問題に応用されている。--物性物理学やのや物理化学のシミュレーションや素粒子物理学の格子ゲージ理論シミュレーションののみならず、統計的手法に基づく情報処理の分野やニューラルネットワークの学習理論などさまざまである。--
本実習では、もっとも基本的なモデルあるイジングモデル(Ising model) を取り上げ、その統計物理学的な解析的法(解析的び数値的方法(数値シミュレーションの方法))を解説し、実際にシミュレーションをおこないさまざまな量を測ることによって、数値シミュレーションの手法を体得することを目的とする。
ある変数とる値が事前に予知されず、確率
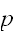 にしたがって出現するとみなすとき、これを確率変数といい
にしたがって出現するとみなすとき、これを確率変数といい

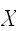 ,
,
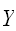 ,
,
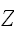 などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と体重などの値の範囲を持った連続型がある。
などの大文字で表現する。確率変数には、サイコロのように有限個の整数などの値をとる離散型と体重などの値の範囲を持った連続型がある。
確率分布は、ある変数がどの値をとる可能性が大きいか、小さいかを実現値と確率の間の関数として現したものである(通常

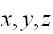 などの小文字で表現する)。ある変数が
などの小文字で表現する)。ある変数が

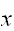 以下である確率を知りたいとき、
以下である確率を知りたいとき、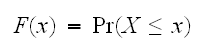 と現す。この関数はある
と現す。この関数はある
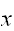 を与えるとこめられることであり、累積分布関数(単に分布関数)と呼ばれる。この関数は単調非減少関数で、有限の値を仮定して次のようのとる。
を与えるとこめられることであり、累積分布関数(単に分布関数)と呼ばれる。この関数は単調非減少関数で、有限の値を仮定して次のようのとる。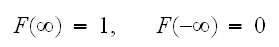 分布関数は、微分可能な場合が多く、その導関数を確率密度関数と呼び、
分布関数は、微分可能な場合が多く、その導関数を確率密度関数と呼び、
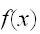 と書くことにする。
と書くことにする。
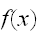 はすべての
はすべての
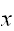 に対して、
に対して、
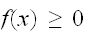 であり、
であり、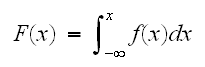 と現される。特に、
と現される。特に、
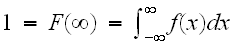 である。また、
である。また、
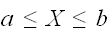 である確率は、
である確率は、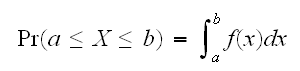 とあらわせる。連続変数の場合、一点の積分はゼロであるので、
とあらわせる。連続変数の場合、一点の積分はゼロであるので、
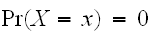 である。
である。
一方、離散変数である場合には、
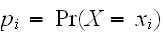 であって、分布関数は積分記号でなく、和記号で現される。
であって、分布関数は積分記号でなく、和記号で現される。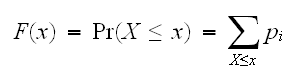
確率変数の分布の様子を示す指標として、分布の中心やバラつきの度合いを示す指標があると便利である。分布の中心を現すものとして、代表的なのが期待値と分散である。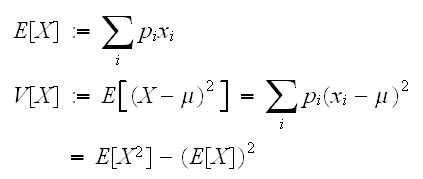 たたし、
たたし、
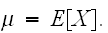 一方、連続変数に対して次で与えられる。
一方、連続変数に対して次で与えられる。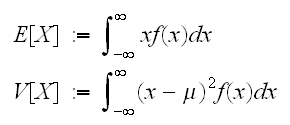
2つの事象
 があるとき、同時に起きる確率
があるとき、同時に起きる確率
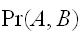 と
と
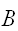 がおきた条件のもとで
がおきた条件のもとで
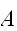 がおきる条件付確率
がおきる条件付確率
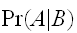 および、そ逆
および、そ逆
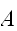 がおきたもとで
がおきたもとで
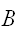 がおきる条件付確率
がおきる条件付確率
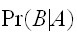 のあいだには、次の関係がある。
のあいだには、次の関係がある。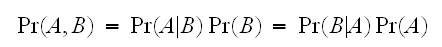 したがって次がえられる。
したがって次がえられる。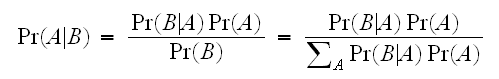
これは、ベイズの定理(ベイズの公式)と呼ばれる。
連続型確率変数
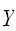 が区間
が区間
![$[a,b]$](graphics/text__35.png) 間で確率密度一定である分布を連続型一様分布(Unifoem
distribution)といい、
間で確率密度一定である分布を連続型一様分布(Unifoem
distribution)といい、
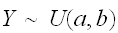 と略記する。これは、確率密度
と略記する。これは、確率密度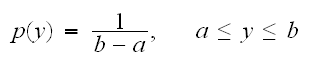 で与えられる。
で与えられる。
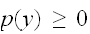 、かつ
、かつ
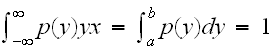 である。
である。
一様分布の平均、分散は次で与えられる。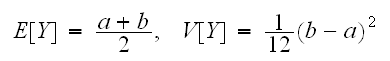
正規分布(nomal
distribuytion)は次のように与えられ、
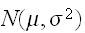 で略記する。
で略記する。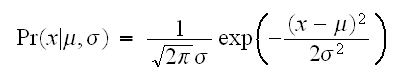 特に、
特に、
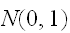 のものを標準正規分布とよび、この分布に従う確率変数は、
しばしば
のものを標準正規分布とよび、この分布に従う確率変数は、
しばしば
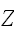 と関数
と関数
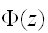 を用いて現される。
を用いて現される。
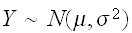 と
と

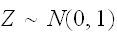 は、
は、
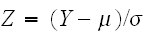 の関係でいつでも変換することができる。正規分布の平均、分散は次で与えられる。
の関係でいつでも変換することができる。正規分布の平均、分散は次で与えられる。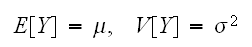
連続型確率変数の組
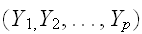 について分布を考える。それぞれの区間
について分布を考える。それぞれの区間
![$(a_{1},b_{1}]$](graphics/text__51.png) 、
、
![$(a_{2},b_{2}]$](graphics/text__52.png) に変数が同時に入る同時確率は、同時確率密度関数
に変数が同時に入る同時確率は、同時確率密度関数 
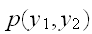 をもちいて
をもちいて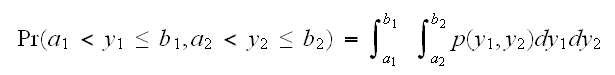 で与えられる。
で与えられる。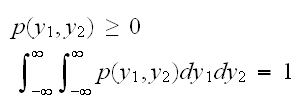 を満たさなければならない。
を満たさなければならない。
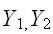 の周辺分布は次のように得られる。
の周辺分布は次のように得られる。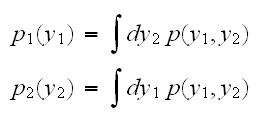 このように、積分によって変数を消去することを周辺化という。
このように、積分によって変数を消去することを周辺化という。

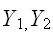 の同時確率密度(同時分布)
の同時確率密度(同時分布)
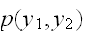 が与えられたとき
が与えられたとき
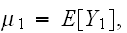

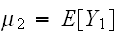 とするとき
とするとき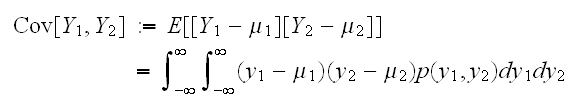 は,
は,
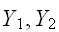 の共分散とよぶ。また、
の共分散とよぶ。また、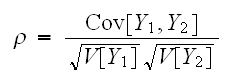 は相関関数と呼ばれる。この量は、しばし
は相関関数と呼ばれる。この量は、しばし
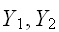 との間の線形相関関係の強さを示す量と解釈され、
との間の線形相関関係の強さを示す量と解釈され、
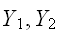 とが独立ならば、必ず
とが独立ならば、必ず
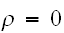 となる。しかし、逆に
となる。しかし、逆に
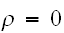 であっても必ずしも、
であっても必ずしも、
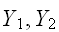 は独立とは限らない。
は独立とは限らない。
統計処理においては、ランダムな誤差を含んだ測定値や観測量の集計を行う。その基本的な、操作である確率の変数の和
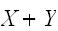 についてその性質を調べる。期待値については、加法性が成立する。
についてその性質を調べる。期待値については、加法性が成立する。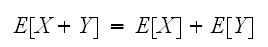 さらに
さらに
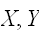 が独立であるときは、分散の加法性が成立する。
が独立であるときは、分散の加法性が成立する。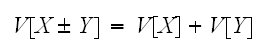

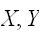 が独立でない時は、
が独立でない時は、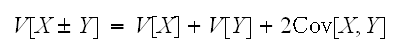 であるの。分散の加法性が成立するためには、無相関であれば十分となる。
であるの。分散の加法性が成立するためには、無相関であれば十分となる。
n個の変数
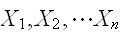 にたいして期待値の加法性が成立する。
にたいして期待値の加法性が成立する。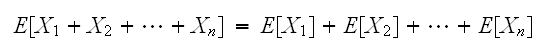 また、
また、
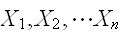 が独立な場合には、分散の加法性が成立する。
が独立な場合には、分散の加法性が成立する。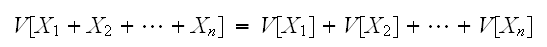
いま、n個の変数
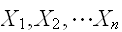 が同一分布に従うとき、これらの期待値、分散を
が同一分布に従うとき、これらの期待値、分散を
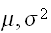 であるとすれば、
であるとすれば、
![$E[X_{k}]=\mu $](graphics/text__82.png) ,
,
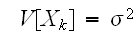 ,
,
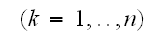 であるので
であるので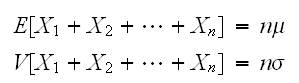 である。したがって標準偏差は、
である。したがって標準偏差は、
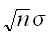 と
と
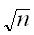 に比例することが重要である。
に比例することが重要である。
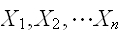 の相加平均(アンサンブル)
の相加平均(アンサンブル)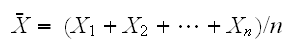 とおくと相加平均の期待値、分散は次で与えられる。
とおくと相加平均の期待値、分散は次で与えられる。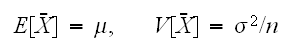
確率変数

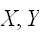 が独立で、それぞれ
が独立で、それぞれ
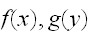 に従うとすると、和
に従うとすると、和

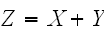 の従う確率分布
の従う確率分布
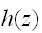 を考える。
を考える。
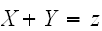 となるのは、
となるのは、
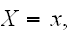

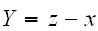 の同時分布のすべての和であるから、離散分布のとき
の同時分布のすべての和であるから、離散分布のとき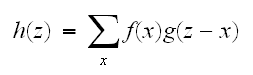 であり、連続分布のときは、和を積分に置き換えればよく
であり、連続分布のときは、和を積分に置き換えればよく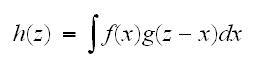 となる。関数
となる。関数
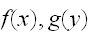 から、
から、
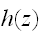 をつくる操作を畳み込みという。
をつくる操作を畳み込みという。
たとえば、
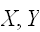 が正規分布
が正規分布
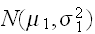 、
、
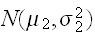 に従うとき、その畳み込み(記号
に従うとき、その畳み込み(記号

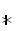 を使って表現する)は、
を使って表現する)は、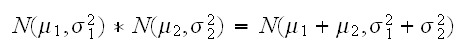 となる。すなわち、
となる。すなわち、
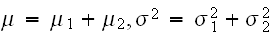 の正規分布になる。
の正規分布になる。
多変数
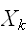 がそれぞれ
がそれぞれ
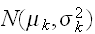 (
(
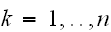 )であるとき、
)であるとき、
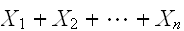 は
は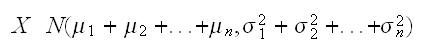 に従う。とくに
に従う。とくに
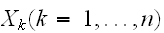 が同一分布
が同一分布
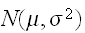 に従うとき、
に従うとき、
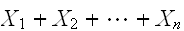 は
は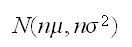 に、
に、
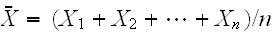 は
は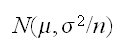 それぞれ従う。
それぞれ従う。
前小節で行った、確率変数の和に対して次の定理がえられる。
いま、
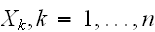 が互いに無相関で期待値
が互いに無相関で期待値
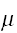 、分散
、分散
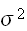 であるとすると、
であるとすると、
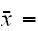

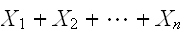 にたいして、
にたいして、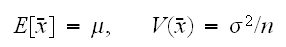 がなりたつ。このときチェビシェフの不等式によって
がなりたつ。このときチェビシェフの不等式によって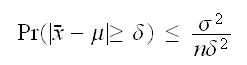 が成立する。ここで、
が成立する。ここで、
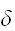 がどんなに小さな正定数であっても、十分大きな
がどんなに小さな正定数であっても、十分大きな
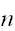 をとることで、式(eq:LargeNth)の右辺はいくらでも小さくすることができる。すなわち、
をとることで、式(eq:LargeNth)の右辺はいくらでも小さくすることができる。すなわち、
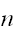 を大きくとることで、
を大きくとることで、
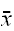 が
が
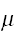 の近辺に集中しているこtろが2次の積率(moment)までの確率でいえる。この事実を大数の弱法則(大数の法則)という。
の近辺に集中しているこtろが2次の積率(moment)までの確率でいえる。この事実を大数の弱法則(大数の法則)という。

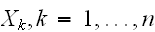 が互いに独立かつ同一の確率分布に従う確率変数列で、
が互いに独立かつ同一の確率分布に従う確率変数列で、
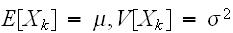 とする。このとき、
とする。このとき、
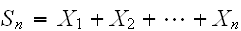 にたいして、つぎが成立する。
にたいして、つぎが成立する。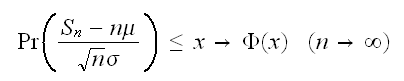 すなわち、
すなわち、
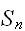 は常に、正規分布に近づいていくことが知られている。これを中心極限定理と呼ぶ。
は常に、正規分布に近づいていくことが知られている。これを中心極限定理と呼ぶ。
統計物理学に基づくモンテカルロシミュレーションに入る前に、モンテカルロ法 Note_1 に基づく数値積分について概観する。モンテカルロ法は、端的にいえば「サイコロを振って積分する方法」ということができる。
はじめに、もっとも簡単な例を考える。積分領域
 と、関数値域
と、関数値域
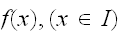 を囲む領域
を囲む領域
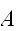 を考え、領域
を考え、領域
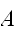 にランダムな点を振る。曲線
にランダムな点を振る。曲線
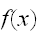 の下側の領域の割合と、領域
の下側の領域の割合と、領域
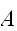 の体積(面積)との積で積分が推定することが出来る。
の体積(面積)との積で積分が推定することが出来る。 この方法は、曲面(曲線)
この方法は、曲面(曲線)
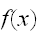 が複雑な形状をしていても、曲線
が複雑な形状をしていても、曲線
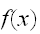 の下側の領域の点の生成と積分を容易に行うことが出来る利点がある。しかし、一般に効率のよい方法ではなく、見積もりの誤差も議論されなければならない。
の下側の領域の点の生成と積分を容易に行うことが出来る利点がある。しかし、一般に効率のよい方法ではなく、見積もりの誤差も議論されなければならない。
一様サンプリングによる、モンテカルロ積分の推定法を天下り的にではあるが導入する。多次元空間の領域
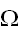 (体積
(体積
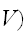 の一様なランダムな点
の一様なランダムな点
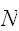 個の点
個の点
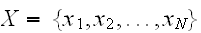 をサンプリングしたとする。モンテカルロの基本定理によれば次の式で推定される。
をサンプリングしたとする。モンテカルロの基本定理によれば次の式で推定される。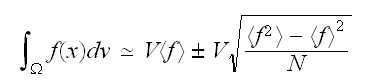 ここで、角括弧は、
ここで、角括弧は、
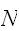 個の点における算術平均を意味する。すなわち、
個の点における算術平均を意味する。すなわち、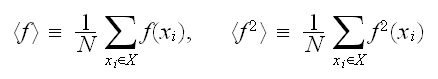 式(eq:MonteI)の
式(eq:MonteI)の
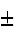 の項は、標準偏差に相当する誤差の推定値であり、厳密な限界を示す誤差ではない。 Note_2 また、誤差がガウス分布である保障もない。大雑把に見積もった値である。
の項は、標準偏差に相当する誤差の推定値であり、厳密な限界を示す誤差ではない。 Note_2 また、誤差がガウス分布である保障もない。大雑把に見積もった値である。
実際の計算を行う際には、与えられた領域
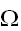 の一様サンプリングされた点と体積
の一様サンプリングされた点と体積
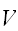 がわかっていることが前提となが、実際の計算できるのは
がわかっていることが前提となが、実際の計算できるのは
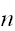 次元直方体の領域など限られた場合である。
次元直方体の領域など限られた場合である。
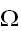 が複雑な形状を持った領域でも、体積の見積もり及び一様サンプリングか容易に行える
が複雑な形状を持った領域でも、体積の見積もり及び一様サンプリングか容易に行える
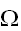 を囲む領域
を囲む領域
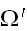 を導入することで、
を導入することで、
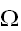 内の点を生成することが可能である。また、領域
内の点を生成することが可能である。また、領域
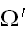 (体積
(体積
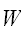 )で定義された関数
)で定義された関数
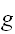 を
を
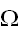 内の点
内の点
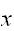 に対して、
に対して、
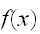 、外の点においてゼロであるように定義すれば
、外の点においてゼロであるように定義すれば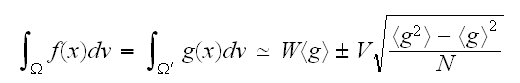 として積分を推定することができる。
として積分を推定することができる。
一様サンプリングの方法は、積分の誤差は
一様サンプリングされた関数の分散を用いて、
![$\sqrt{V[f(x)]/N}$](graphics/text__167.png) で与えられた。これは、非積分関数の値が大きく変化をする場合には、推定誤差が大きくなってしまうことを意味している。このような状況を改善するために積分を次のように書き換えることを考える。
で与えられた。これは、非積分関数の値が大きく変化をする場合には、推定誤差が大きくなってしまうことを意味している。このような状況を改善するために積分を次のように書き換えることを考える。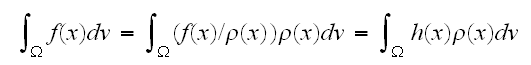 とする。いま、一様な重み
とする。いま、一様な重み

 でサンプリングする代わりに、重み
でサンプリングする代わりに、重み
 でサンプリングができるとしたらどうなるであろうか。
でサンプリングができるとしたらどうなるであろうか。
このようサンプルされた点は、確率分布
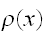 で点が生成することに対応する。確率分布であるので
で点が生成することに対応する。確率分布であるので
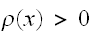 であって、
であって、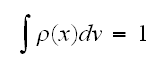 を満たす関数である。いま、式(eq:EV-Ensamble)によれば、
を満たす関数である。いま、式(eq:EV-Ensamble)によれば、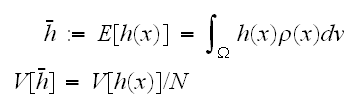 であるから、積分
であるから、積分
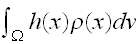 の値とその誤差は、
の値とその誤差は、
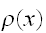 分布に従うサンプリング点
分布に従うサンプリング点
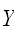 で関数の値
で関数の値
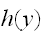 の期待値と分散で与えられる。
の期待値と分散で与えられる。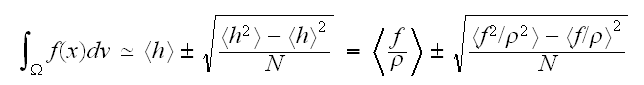 一様サンプリングの場合は、
一様サンプリングの場合は、
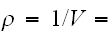 一定の場合である。
一定の場合である。
この表式は
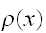 の選び方によらない。一様サンプリングの方法を改善するために、もっとも効率のよい
の選び方によらない。一様サンプリングの方法を改善するために、もっとも効率のよい
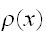 の選び方を求めよう。そのような
の選び方を求めよう。そのような
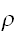 は分散が与えられた
は分散が与えられた
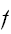 にたいして最小になるように選べばよい。すなわち、拘束条件(eq:ProbCond)をみたし、
にたいして最小になるように選べばよい。すなわち、拘束条件(eq:ProbCond)をみたし、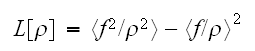 が最小になるような
が最小になるような
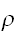 を求めれよい。そのような
を求めれよい。そのような
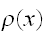 はラグランジュの未定乗数つきの変分
はラグランジュの未定乗数つきの変分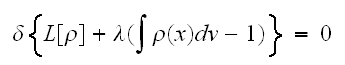 で与えられる。これを解くと
で与えられる。これを解くと
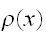 は次の最適解が得られる。
は次の最適解が得られる。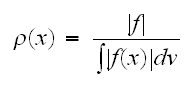
実際に重点サンプリングでモンテカルロ積分を行うには、
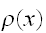 の分布を与えるアルゴリズムを開発しなければならない。この節では、一般の
の分布を与えるアルゴリズムを開発しなければならない。この節では、一般の
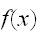 に対する重点サンプリングのアルゴリズムについてふれることはしない。重点サンプリング法を拡張した、適応型モンテカルロ積分の方法として、VEGASアルゴリズムが知られている。(たとえば、Numerical
Recipies in C/C++ NRinC/C++
を参照)。
に対する重点サンプリングのアルゴリズムについてふれることはしない。重点サンプリング法を拡張した、適応型モンテカルロ積分の方法として、VEGASアルゴリズムが知られている。(たとえば、Numerical
Recipies in C/C++ NRinC/C++
を参照)。
本自習では、統計力学のモンテカルロシミュレーションが、多次元の重点サンプリングの分布関数を生成するアルゴリズムを与えるあたること、さまざまな物理量を測ることが重点サンプリングによる多次元積分を実行することに対応することをみる。
多数の要素が互いに影響を及ぼしあっている(相互作用している)とき、どのようなマクロな性質を持つかを解明するのが統計力学の重要な課題である。たとえば、水(
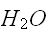 )が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。
)が、氷、水、水蒸気を温度や圧力などの環境でマクロな性質が大きく異なる状態を取る。このような急激な変化(相転移)を理解する(水の状態を記述する理論ではないが)最も基本的なモデルとして、Isingモデルを導入する。

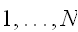 までの番号づけれれた格子点(site)に,値を持つ場を考えよう。格子点は、結晶の原子の配置でもよいし、(白黒)画像のピクセルやニューロン(神経細胞)でもよい。ここでは、
までの番号づけれれた格子点(site)に,値を持つ場を考えよう。格子点は、結晶の原子の配置でもよいし、(白黒)画像のピクセルやニューロン(神経細胞)でもよい。ここでは、
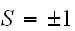 の2値を持つ、Ising
スピン(spin)を対応させたモデルを考えることにする。磁性体のモデルでは、
の2値を持つ、Ising
スピン(spin)を対応させたモデルを考えることにする。磁性体のモデルでは、
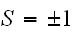 は、原子レベルの磁石(のNSの向き)が、上下のいずれを向いているかをあらわしている。いま、お互いに隣り合ったサイト同士
は、原子レベルの磁石(のNSの向き)が、上下のいずれを向いているかをあらわしている。いま、お互いに隣り合ったサイト同士
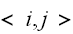 が相互作用するとして、相互作用のエネルギーとして、
が相互作用するとして、相互作用のエネルギーとして、
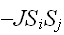 を考える。
を考える。
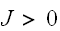 の時、
の時、
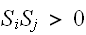 のとき、スピンが揃うときがエネルギーが低くなり安定である。一方、
のとき、スピンが揃うときがエネルギーが低くなり安定である。一方、
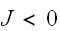 のときは、
のときは、
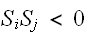 のとき、スピンがお互い反対向きのときが、安定となる。また、磁性体のときにおける外部磁場
のとき、スピンがお互い反対向きのときが、安定となる。また、磁性体のときにおける外部磁場
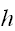 との相互作用
との相互作用

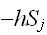 を付け加えた系を考える。統計力学では、系全体のエネルギー取り扱うハミルトンの関数(ハミルトニアン)を用いて系を記述する。
を付け加えた系を考える。統計力学では、系全体のエネルギー取り扱うハミルトンの関数(ハミルトニアン)を用いて系を記述する。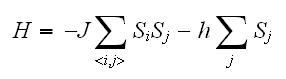 Isingモデルにおいては、系の相互作用は最近接相互作用でその強さが共通であるが、相互作用の形がどのようになるかは問題によって異なることを注意しておく。
Isingモデルにおいては、系の相互作用は最近接相互作用でその強さが共通であるが、相互作用の形がどのようになるかは問題によって異なることを注意しておく。
統計力学の処方箋(詳しくは、統計力学とIisngモデルで解説)によると、ハミルトニアンが与えられると、スピンがとる配位の確率分布は、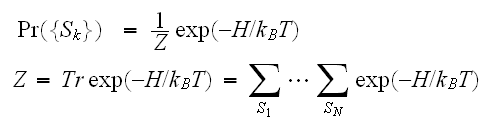 で与えられる。ここで
で与えられる。ここで
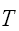 は温度、
は温度、
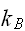 はボルツマン(Boltzmann)
の定数である。
はボルツマン(Boltzmann)
の定数である。
Isingモデルの統計力学の解析の例として画像修復の問題を紹介する。
雑音によって乱れた不完全な画像が与えられたとき現画像を推定する問題は、ベイズの公式を用いて、確率論を用いた画像修復の問題として、統計力学の手法を応用することができる。2次元の白黒の画像を考えると、各ピクセルは、格子点上のイジングスピン
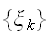 と対応付けることができる。元の画像
と対応付けることができる。元の画像
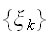 は、受信側では
は、受信側では
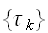 であらわすこととする。画像は、伝送の間に乱され確率
であらわすこととする。画像は、伝送の間に乱され確率 
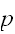 で、ビットが反転すると、
で、ビットが反転すると、
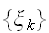 が与えられたときの
が与えられたときの
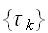 の出現確率は次で与えられる。
の出現確率は次で与えられる。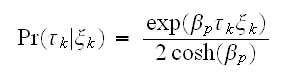 各サイトでビット反転が独立であるとすると、全体では、
各サイトでビット反転が独立であるとすると、全体では、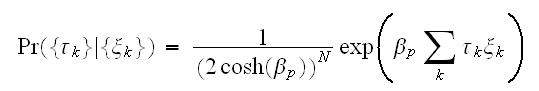 である。画像修復では、劣化画像
である。画像修復では、劣化画像
 から、原画
から、原画
 を推定するもんだいであるので、推定画像を
を推定するもんだいであるので、推定画像を
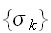 と書くとすると、ベイズの公式を用いて次のようにかける。
と書くとすると、ベイズの公式を用いて次のようにかける。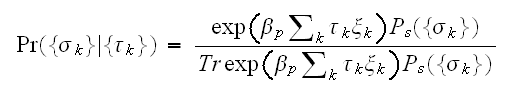 これは、劣化画像
これは、劣化画像
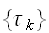 及び、事前知識
及び、事前知識
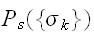 が画像修復に必要であることを示している。しかし、
が画像修復に必要であることを示している。しかし、
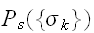 が正確にわからなくても、モデル分布
が正確にわからなくても、モデル分布
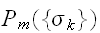 を
を
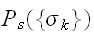 の代わりに使うこととする。
の代わりに使うこととする。
ここでは、モデル分布
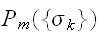 を次のように考えて構成する:白の背景の中に孤立した黒の点がある場合は、もともとあった黒であるよりも、白の点がノイズによって反転した可能性が大きいと考える。このことを、隣り合うピクセル対は、違う状態であるよりもおなっ状態である確率が高いと解釈し、次の事前分布のモデルを導入する。
を次のように考えて構成する:白の背景の中に孤立した黒の点がある場合は、もともとあった黒であるよりも、白の点がノイズによって反転した可能性が大きいと考える。このことを、隣り合うピクセル対は、違う状態であるよりもおなっ状態である確率が高いと解釈し、次の事前分布のモデルを導入する。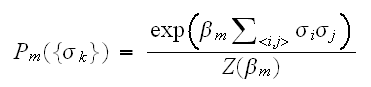 ここで、
ここで、
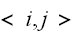 は隣同士のピクセルについての和であり、
は隣同士のピクセルについての和であり、
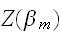 は企画化因子である。これはイジングモデルをあらわす。したがって、式(eq:BaysePix)へ事前分布を代入すると、画像修復の確率分布(事後分布)は、Ising模型にランダムな磁場がかかったスピン系の統計力学の問題となった。
は企画化因子である。これはイジングモデルをあらわす。したがって、式(eq:BaysePix)へ事前分布を代入すると、画像修復の確率分布(事後分布)は、Ising模型にランダムな磁場がかかったスピン系の統計力学の問題となった。
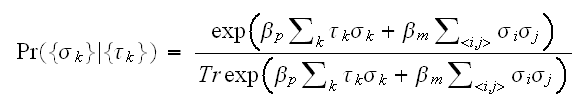 最大事後確率の考え方にたてば、式(eq:MAPPiX)を最大にする
最大事後確率の考え方にたてば、式(eq:MAPPiX)を最大にする
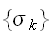 が修復画像となる。
が修復画像となる。
Donald E. Knuth, "The art of Computer Programing" Vo2. Seminumerical Alogorithm. Addidon-Wesly, 2nd edition 1981. (サイエンス社からの邦訳あり)
奥村晴彦 「C言語によるアルゴリズム事典」 技術評論社ISBM4-87408-414-1
伏見正則「乱数」東京大学出版,1989
G.E.P. Box amd M.E. Muller, An. math. Statist. 26: 610 (1958); G.Mardagla and T.A.Bray, Rev. Soc. Ind. Appl. Math. 6 260(1964)
Numerical Recipies in C/C++ the art of Scientific Computing 2nd edition, W.H. Press 他著、Cambridge Press