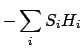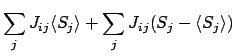Next: 対称性の自発的破れ
Up: 2次元 Ising モデル
Previous: 2次元 Ising モデル
平均場理論では、ある格子点上のスピンは、外から与えられた
場(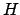 )に加えて、系のスピンがつくり出す磁場からの作用を
受けるものとする。
即ち、格子点
)に加えて、系のスピンがつくり出す磁場からの作用を
受けるものとする。
即ち、格子点 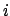 のスピン
のスピン 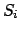 は、磁場
は、磁場
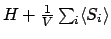 を受けるものとし、この時の
を受けるものとし、この時の
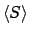 の値を
self-consistent に求める。
の値を
self-consistent に求める。
Site 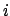 での局所的磁場を
での局所的磁場を 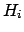 と書くと、
と書くと、
ここで、平均場理論では、第2式の右辺第3項、即ち
揺らぎの効果をを無視する。
d-次元の正方格子の場合、
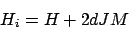 |
(48) |
となる。
ここで 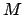 は
は
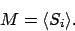 |
(49) |
であり、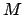 に対する self-consistent な関係式は
に対する self-consistent な関係式は
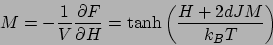 |
(50) |
となる。
外場 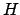 が無い場合でも、自発磁化の効果が第2項に存在する。
が無い場合でも、自発磁化の効果が第2項に存在する。
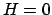 とすると、
とすると、
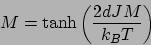 |
(51) |
であるが、これを満たす 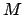 は、
は、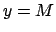 と
と
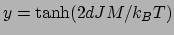 との交点として求めることができる
(Figure 1参照)。
との交点として求めることができる
(Figure 1参照)。
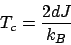 |
(52) |
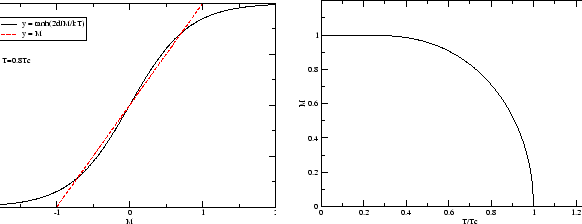
よりも高い温度 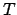 では、交点は
では、交点は 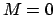 にしか存在せず、
自発磁化は生じない。
にしか存在せず、
自発磁化は生じない。
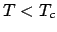 では
では 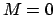 以外にも、
Eq. (51)を満たす
以外にも、
Eq. (51)を満たす 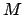 が存在する。
が存在する。
Figure 1:
2次元Isingモデルの平均場近似による解析。
左図は、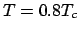 の場合について、
Eq. (51)を満たす磁化
の場合について、
Eq. (51)を満たす磁化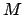 を求める様子を
示した。
右図は
を求める様子を
示した。
右図は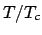 に対する磁化
に対する磁化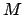 のプロット。
のプロット。
 |
Hideo Matsufuru
2006-06-16
![]() )に加えて、系のスピンがつくり出す磁場からの作用を
受けるものとする。
即ち、格子点
)に加えて、系のスピンがつくり出す磁場からの作用を
受けるものとする。
即ち、格子点 ![]() のスピン
のスピン ![]() は、磁場
は、磁場
![]() を受けるものとし、この時の
を受けるものとし、この時の
![]() の値を
self-consistent に求める。
の値を
self-consistent に求める。
![]() での局所的磁場を
での局所的磁場を ![]() と書くと、
と書くと、